Why rounding error matters even the amount of error seems to be small ?
Let’s imagine we have an e-commerce system. It tracks price values and discount values for items. Example records are
{item_id: item1, price: 1000, discount: 10},
{item_id: item2, price: 2000, discount: 30}, …
Now, you have to update the records. We will receive new price value for specific item_id. For example,
{item_id: item1, price: 860}
is an event you have to process. Thing is we have to update discount values upon the price change while keeping the original discount percentage.
For example, we’ll update discount value from 10 to 9 for the above price updates according to calculation like (old_discount/old_price) * current_price = round ((860 / 1000 ) * 10) = round(8.6) = 9. Note that both price and discount values are integer.
Mathematical formula for the discount update is simple if we don’t have rounding.
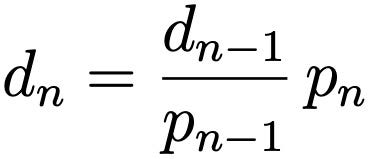
, where d_n is discount value after n time updates and p_n is the price value after n time updates.
In equation 1, the result should preserve the original discount percentage. It is shown in the following mathematical calculation.
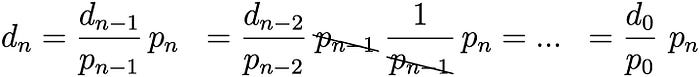
However, in reality, we have rounding. Then, something happens here. For example, if there was price updates of 940 before updates of 860 in the previous example, the final discount value will be different than the previous calculation.
{price_0: 1000, discount_0: 10}
{price_1: 940, discount_1 = round((940/1000) * 10)= round(9.39) = 9}
{price_2: 860, discount_2 = round((860/940) * 10)= round(8.23) = 8}
In the previous calculation, where we only had one price updates of 860, the discount value was 9. But, for the above price updates history, we have 8 for the final discount value even it has the same price of 860.
How rounding errors affect the final result
As we saw in the previous section, rounding matters. Equation1 in the previous section has to be updated to take the rounding error into account.
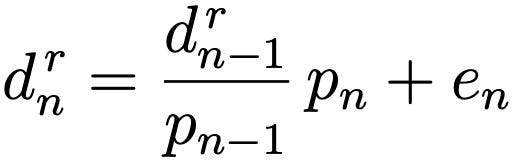
, where d^r_n is discount value after n time updates with rounding errors, and e_n is a rounding error after n time updates. Rounding error e_n is between -0.5 and 0.5 .
Interesting thing is that even each rounding error is bounded to between -0.5 and 0.5, it might have bigger effect as it is accumulated over multiple iteration. By substituting equation2 recursively, we can see this accumulation in mathematical equations.
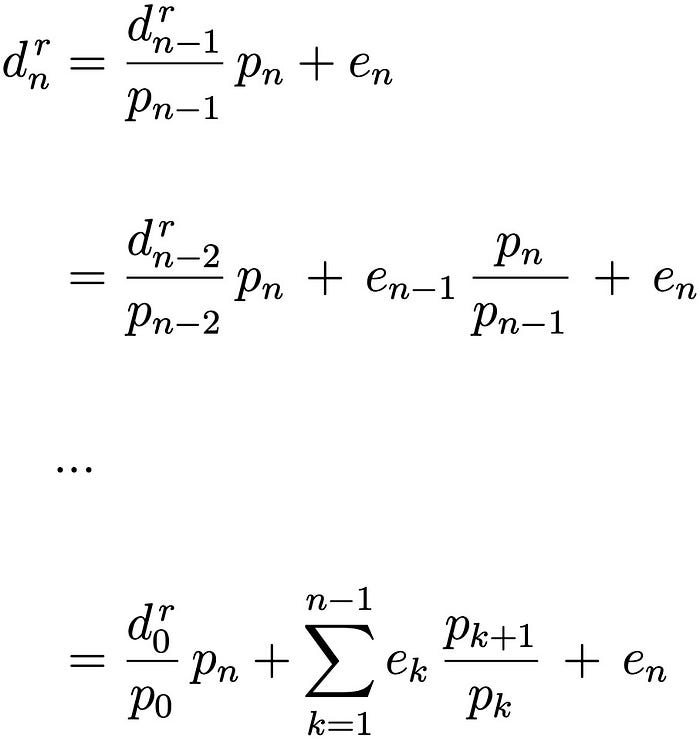
Here, we are seeing all the errors (with coefficients) sums up. The coefficient (p_k+1 / p_k) is the ratio of price changes for (k+1)-th iteration. As it sums over 1…n-1, the order of total error is O(n).
Let’s evaluate the value range of coefficients. In general, it could be arbitrary values. For example, if price get 10 times larger, errors might amplified by 10.
Sometime, we might be able to bound the amount of price change. For example if price updates never get more than 200%, the coefficients for rounding error (p_k+1 / p_k) would be always less than 2. In that case, we can have more strict evaluation for the total rounding errors.
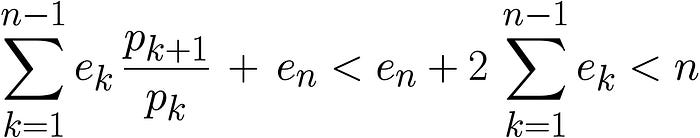
The amount of total rounding error is bounded to n, where n is the number of price updates.
Avoid rounding errors in the schema design
Avoiding the rounding errors is not if we can update schema of the datastore. We might want to add new field ‘discount_percentage’ to preserve the original discount percentage.
{item_id: item1, price: 1000, discount: 10, discount_percentage: 0.01 }
or can update the type of discount from integer to type with sufficient precision (e.g. BigDecimal in Java).
{item_id: item1, price:1000, discount: “10.000”}
Though this change requires clients logic to do rounding by theirselves.
In conclusion, don’t underestimate rounding errors. It should be within 0.5 at maximum for each rounding. However, it might accumulate over multiple iteration and end up arbitrary amount of difference.
